1) La détermination du cercle oculaire revient à déterminer l'image de la lentille d'entrée.

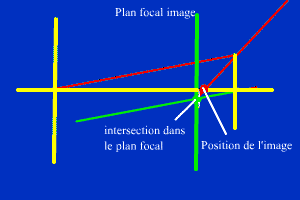
On trace un rayon quelconque issu du centre de la première lentille (en rouge).
On trace un rayon parallèle passant par le centre optique de la deuxième lentille (en vert) qui n'est pas dévié.
Le rayon rouge sortant de la deuxième lentille et le rayon vert sortant ont leur point d'intersection dans le plan focal image de la deuxième lentille.
La pente du rayon rouge sortant est six fois celle du rayon rouge entrant, donc l'image est placée à (5/6)F c'est à dire 7,1 cm avant la lentille.
Le grandissement est de 5/36 la taille de l'image est de 0,4 cm.

2) intérêt du dispositif

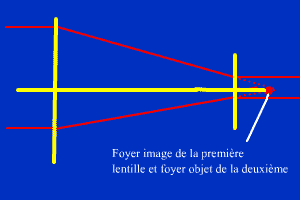
Le système réalisé est afocal. Des rayons entrant parallèles sortent parallèles.
Le grandissement de n'importe quel objet est donc de 1/6. Cela n'a pas d'importance pour l'observation astronomique car l'image n'est pas projetée. On aura une concentration du flux sur une surface plus faible donc l'éclairement sera plus important et l'image plus lumineuse que l'objet.

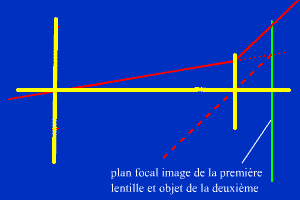
La construction du trajet d'un rayon incident incliné par rapport à l'axe optique montre que l'inclinaison de sortie a été multipliée par 6.
On peut modélisée la lune par un objet à l'infini, c'est à dire des faisceaux de rayons parallèles. L'angle maximum entre ces faisceaux est le diamètre angulaire apparent de la lune 3500/385000=0.0091=31' ou celui d'un cratère 85/385000=0.8'. La taille du cratère sera donc de 5', visible par l'observateur. Il sera grossit d'un facteur 6
On pourra observer Archimède. Pour Michelson ce sera plus difficile car il est sur la face cachée de la lune!

3)

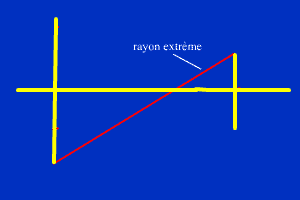Pour déterminer le diamètre apparent maximum observable, il suffit de considérer les rayons extrèmes:
2(3+0,5)/50=8°.

On peut observer la lune en entier (3°)