équation
de Maxwell-Gauss | Relation local reliant les variations spatiales du champ électrique à la densité volumique de charges |
| La forme globale lui correspondant s'appelle le théorème de Gauss.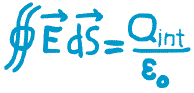 Le deuxième membre de l'égalité faisant intervenir la charge intérieure à la surface fermée d'intégration. |
| On peut en donner une formulation locale en présence de distribution surfacique de charges: la relation de passage pour le champ électrique |
| Associée à l'équation de Maxwell Faraday électrostatique, elle permet de déterminer les lois de l'électrostatique |