La découverte des fractales
Au début du XXième siècle, Un certain nombre de mathématiciens français, dont fasait partie Szolem mandelbrojt un oncle de Benoît Mandelbrot, fondèrent un groupe. Ils appelèrent se groupe Bourbaki, et entreprirent d'écrire en commun un traité, le plus complet possible, de mathématiques. Peut être en réaction contre Poincaré, pour qui la rigueur n'était pas fondamentale, ils basèrent leur traité sur la rigueur et l'abstraction la plus complète.
Cette démarche est aujourd'hui sévèrement critiquée:
| On l'accuse de tuer l'esprit d'initiative par son exigence continuelle de rigueur. | |
| On lui reproche d'enfermer les mathématiques dans le carcan de la théorie des ensembles par son dogmatisme. | |
| Son haut niveau d'abstraction couperait les mathématiques du monde. |
Ces critiques me laissent perplexe.
| Il est relativement rare que l'on laisse libre cours à l'esprit d'initiative d'un jeune chirurgien ou d'un apprenti boulanger. La rigueur est un pilier important des mathématiques, le jeune mathématicien doit y être initié. On monte rarement de bons mur en empilant de manière désordonnée des pierres prises au hasard. | |
| Bien sûr, tous les scientifiques savent qu'aborder un problème d'une seule façon conduit rarement à de nouvelle découvertes. Mais les ouvrages de Bourbaki ne sont pas une philosophie, seulement un outils fantastique mettant à plat les connaissances mathématiques de l'époque, une des bases permettant de mener plus loin les mathématiques. Il y a eu, à mon sens, des excès c'est certain, mais si trop de bourbakisme n'est pas une bonne chose, trop peu serait catastrophique. | |
| La présentation que fait Bourbaki des mathématiques est abstraite, elle en fait un objet séparée des autres sciences, et alors ? On peut apprendre à peindre (et si l'on veut faire les choses correctement, il faut un minimum de rigueur) pour le coté pratique de la chose, mais aussi pour ce faire plaisir, pour l'art. Pourquoi refuser aux mathématiques ce que l'on accorde à la peinture, l'écriture... |
Les premières fractales immaginées étaient des courbes construites pour malmener
l'intuition des mathématiciens sur la notion de dérivabilité, elle n'avait pas pour but
une quelconque description.
Mandelbrot était à l'aise avec une représentation géométrique des mathématiques, le
fait d'avoir profité de l'influence de son oncle et d'études à l'école polytechnique
ne lui a-t-il pas ouvert des horizons et permis de voir ces nouveaux objets?
Dans les progrès de la théorie du chaos, les mathématiciens et physiciens
français ont joué et jouent un rôle loin d'être négligeable. La formation
scientifique française, jugée souvent trop académique, n'y serait pas pour quelque
chose ?
Le dogme, en science, est important car la science progresse au fur et à mesure des générations, il faut pouvoir s'appuyer sur quelque chose de clair et de solide. Mais ce dogme n'est pas un aboutissement ou une quelconque vérité, c'est un tremplin qui permettra de s'élever plus haut que ses prédécesseurs.
Obtentions de fractales
Pour obtenir une courbe fractale, on procède souvent par itération.
Par exemple, on construit une courbe simple, à l'aide d'une méthode simple. puis, avec des parties de cette courbe, on recommence l'opération.
On définit une suite itérative à l'aide d'une fonction, puis on cherche les paramètres ou les germes de la suite pour lesquels la suite possède une propriété particulière.
On a représenté, ci-dessous, l'ensemble de Mandelbrot, en grossissant des détails de la figure

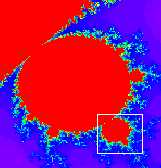
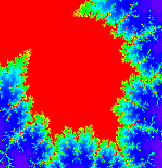
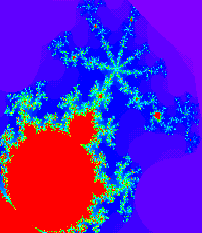
On peut voir d'autres fractales dans un site dédié
Propriétés des fractales
Les courbes fractales sont très irrégulière. Quand on les regarde dans le détail, il n'est pas possible de trouver une échelle où elle soit lisse. En fait la meilleur façon de représenter une fractale serait de tracer une courbe possédant une certaine épaisseur. On voit apparaître une propriété importante des courbes fractales, ce sont des traits tellement enchevétré qu'on pourrait les prendre pour des surfaces. Une droite est un objet de dimension 1, un plan de dimension 2, une fracale peut prendre une dimension généralisée comprise entre 1 et 2 (celle de la courbe de Von Koch est de 1,26 et celle de la frontière de l'ensemble de Mandelbrot est de 2).
Certaines fractales, comme la courbe de Von Koch, sont autoaffines, cela signifie que l'observation d'une petite zone de cette courbe permet de retrouver la structure entière de la courbe, on retrouve la courbe dans n'importe laquelle de ses parties comme des poupées gigognes sans fin.