Introduction au problème
Nous allons étudier un système dynamique pouvant donner des solutions périodiques.
On sait, alors, qu'a intervalles réguliers, égaux à la période T, les variables
reprendront la même valeur.
Pour résoudre le problème, on s'attache à déterminer une section de Poincaré dans l'espace des phases.
Il s'agit de relier pour une variable sa valeur à l'instant nT en fonction de celle à l'instant (n-1)T. On construit alors une suite de valeurs dépendant de la valeur précédente: une suite itérative
Résolution du problème
Notre suite itérative sera définie par une fonction particulière qui servira à trouver la valeur du terme de rang n (instant nT) en fonction du terme de rang (n-1) (instant (n-1)T). Il faut choisir une fonction non linéaire si l'on veut voir apparaître le chaos. On prend f(x)=4rx(1-x) avec 0<x<1.
| Pour des valeurs faibles du paramètre r le système est périodique, sur le segment des valeurs possibles l'attracteur est un point. |
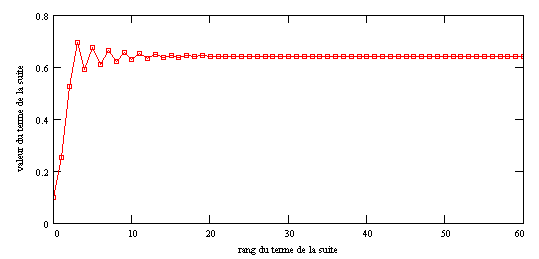
| Dès que r atteint 0.75 la période du système est multipliée par 2, l'attracteur est constitué de deux points. |
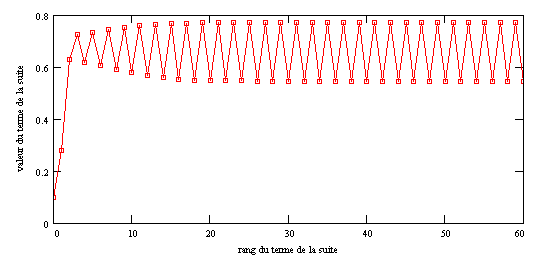
| L'augmentation du paramètre conduit à des doublements successifs de la période. ( figure pour r=0.88) |
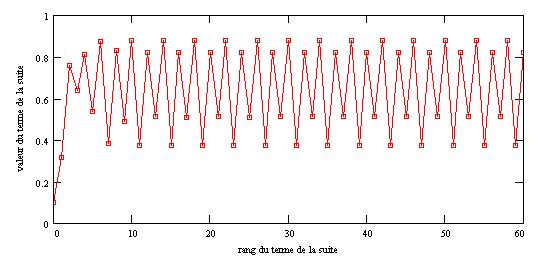
| ces doublements sont de plus en plus rapprochés et pour r=0.8924864... on atteint un régime chaotique. (figure pour r=0.97) |
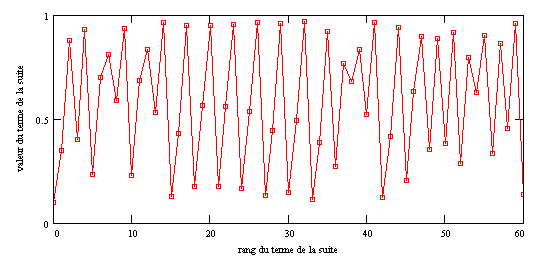
Comportement du système
On peut analyser le comportement du système en déterminant sa période en fonction du paramètre r.
| Le système reste périodique pour r<0.75 |

| En agrandissant la zone proche de 1, on remarque l'enchevêtrement des zones
périodiques de différentes périodes, entrecoupée par des zones (en rouge) où la
périodicité n'a pu être détectée. On remarque une zone, pour r voisin de 0.96, où règne une certaine accalmie. |

| Les deux agrandissements suivants, mettent en évidence le caractère fractale de l'ensemble représenté. Quelque soit l'échelle, on remarque une nette ressemblance entre les diverses figures. |

