entraîne
l'existence d'un potentiel scalaire par:L'équation de Maxwell-Faraday en régime permanent, entraîne
l'existence d'un potentiel scalaire par:
 | Cette relation possède aussi une formulation intégrale: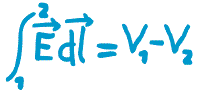
qui est un des base de l'électrocinétique |
| Ce potentiel est relié, par son Laplacien, aux charges par l'équation de Poisson: |
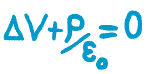
| Dans le cas d'une distribution de charges finie, on obtient les solutions suivantes: |
et 
qui permet de retrouver la loi de Coulomb
d'interaction entre deux particules chargées immobiles
| On est pas sans remarquer la profonde ressemblance avec le potentiel vecteur de la magnétostatique, ressemblance encore renforcée en régime variable. |