dans un domaine de fréquence dépassant largement le Téra hertz (1THz=1012Hz).
On constate, dans les conducteurs, que le terme appelé courant de
déplacement dans l'équation de Maxwell Ampère
est négligeable devant le terme de courant. Ceci se traduit expérimentalement
par la validité de la loi des noeuds locale:
dans un domaine de fréquence dépassant largement le Téra hertz (1THz=1012Hz).
La loi des noeuds globale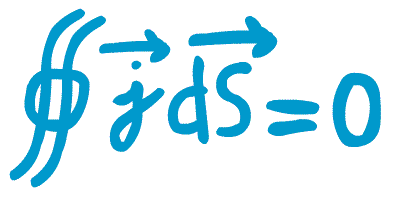 
restera valable si, de plus, la taille du circuit reste inférieur à la
longueur d'onde correspondant à la fréquence maximale du champ
électromagnétique. 30cm pour le Giga hertz , 6000km pour le 50Hz.
Il faut modifier les équations de Maxwell en enlevant le terme de courant de déplacement dans l'équation de Maxwell Ampère.
Les équations reliant le champ magnétique aux courants sont les même qu'en magnétostatique. Toutes les propriétés du champ magnétique vis à vis des courants, sont alors celle du champ magnétostatique.
Ces équations sont incompatibles avec la conservation de la charge. Fort
heureusement, elles seront utilisée dans des conducteurs neutres. On pourra
alors remplacer l'équation de Maxwell Gauss
par 
.
Si les courants sont fixés, alors le champ magnétique est déterminé, et le
champ électrique aussi. Il a la même structure formel vis à vis des
variations temporelles du champ magnétique que le champ magnétostatique vis à
vis des courants. C'est un champ à
rotationnel.
On trouve aussi des applications pour les lois de l'ARQP dans les conducteurs ohmiques